解答题
(16)(本小题满分14分)
如图,在正三棱柱![]() 中,AB=3,
中,AB=3,![]() ,M为
,M为![]() 的中点,
的中点,
P是BC上一点,且
由P沿棱柱侧面经过棱![]() 到M的最短路线长为
到M的最短路线长为![]() ,设这条最短路线与
,设这条最短路线与![]()
的交点为N,
求: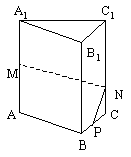
(I)该三棱柱的侧面展开图的对角线长
(II)PC和NC的长
(III)平面NMP与平面ABC所成二面角(锐角)的大小
(用反三角函数表示)
本小题主要考查直线与平面的位置关系、棱柱等基本知识,考查空间想象
能力、逻辑思维能力和运算 能力。满分14分。
解:(I)正三棱柱![]() 的侧面展开图是一个长为9,宽为4的矩形,
的侧面展开图是一个长为9,宽为4的矩形,
其对角线长为![]()
(II)如图1,将侧面![]() 绕棱
绕棱![]() 旋转
旋转![]() 使其与侧成
使其与侧成![]() 在同一平面上,
在同一平面上,
点P运动到点![]() 的位置,
连接
的位置,
连接![]() ,则
,则![]() 就是由点P沿棱柱侧面经过棱
就是由点P沿棱柱侧面经过棱![]() 到
到
点M的最短路线
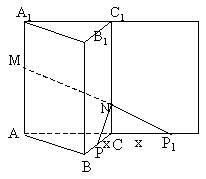
设![]() ,则
,则![]() ,在
,在![]() 中,由勾股定理得
中,由勾股定理得![]()
求得![]()
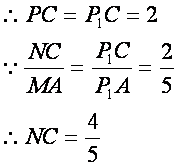
(III)如图2,连结![]() ,则
,则![]() 就是平面NMP与平面ABC的交线,
就是平面NMP与平面ABC的交线,
作![]() 于H,又
于H,又![]() 平面ABC,连
结CH,由三垂线定理得,
平面ABC,连
结CH,由三垂线定理得,![]()
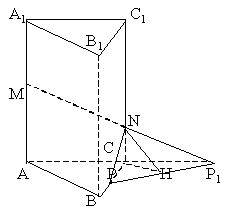
![]() 就是平面NMP与平面ABC所成二面角的平面角(锐角)
就是平面NMP与平面ABC所成二面角的平面角(锐角)
在![]() 中,
中,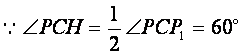
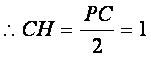
在![]() 中,
中,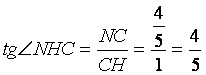
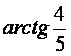
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。