解答题

22．（本小题满分14分）已知数列的前项和满足.

（1）写出数列的前三项；

（2）求数列的通项公式；

（3）证明：对任意的整数，有 .

本小题主要考查数列的通项公式，等比数列的前n项和以及不等式的证明.

考查灵活运用数学知识分析问题和解决问题的能力.满分14分.

    （Ⅰ）解：由

由

由

（Ⅱ）解：当时，有

  …… 

所以 

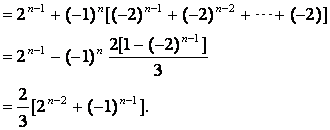
经验证a₁也满足上式，所以 

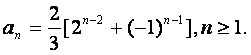
（Ⅲ）证明：由通项公式得

当且n为奇数时， 

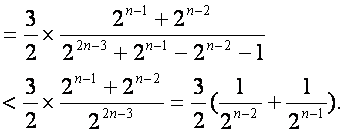
当为偶数时，

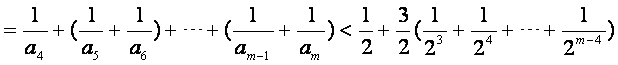
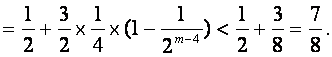
当为奇数时，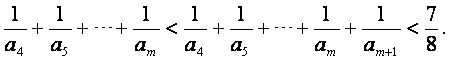

所以对任意整数m>4，有