解答题
22.(本小题满分12分)
已知方向向量为v=(1,![]() )的直线l过点(0,-2
)的直线l过点(0,-2![]() )和
)和
椭圆C: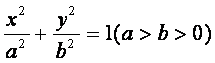 的焦点,且椭圆C的中心关于直线l的对称点
的焦点,且椭圆C的中心关于直线l的对称点
在椭圆C的右准线上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在过点E(-2,0)的直线m交椭圆C于点M、N,
满足![]() cot∠MON≠0(O为原点).若存在,求直线m的方程;
cot∠MON≠0(O为原点).若存在,求直线m的方程;
若不存在,请说明理由.
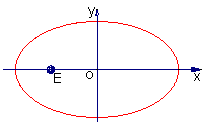
本题考查直线、椭圆及平面向量的基本知识,平面解析几何的基本方法和综合解题能力
(I)解法一:直线![]() ,
①
,
①
过原点垂直![]() 的直线方程为
的直线方程为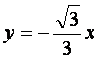 ,
②
,
②
解①②得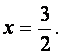
∵椭圆中心(0,0)关于直线![]() 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,
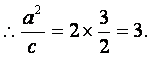
∵直线![]() 过椭圆焦点,∴该焦点坐标为(2,0).
过椭圆焦点,∴该焦点坐标为(2,0).
![]() 故椭圆C的方程为
故椭圆C的方程为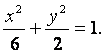 ③
③
解法二:直线![]() .
.
设原点关于直线![]() 对称点为(p,q),则
对称点为(p,q),则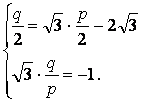 解得p=3.
解得p=3.
∵椭圆中心(0,0)关于直线![]() 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,
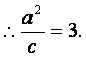 ∵直线
∵直线![]() 过椭圆焦点,∴该焦点坐标为(2,0).
过椭圆焦点,∴该焦点坐标为(2,0).
![]() 故椭圆C的方程为
故椭圆C的方程为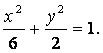 ③
③
(II)解法一:设M(![]() ),N(
),N(![]() ).
).
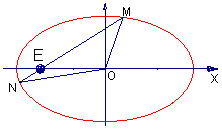 当直线m不垂直
当直线m不垂直![]() 轴时,直线
轴时,直线![]() 代入③,整理得
代入③,整理得
![]()
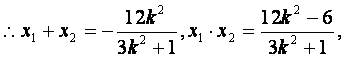
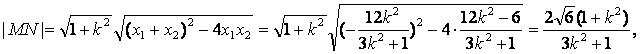
点O到直线MN的距离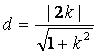
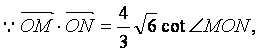 即
即 ![]()
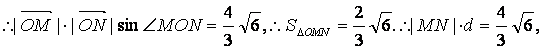
 即
即![]()
整理得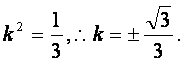
当直线m垂直x轴时,也满足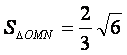 .
.
故直线m的方程为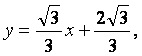
或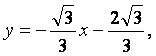 或
或![]()
经检验上述直线均满足![]() .
.
所以所求直线方程为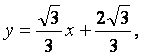 或
或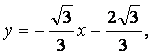 或
或![]()
解法二:设M(![]() ),N(
),N(![]() ).
).
当直线m不垂直![]() 轴时,直线
轴时,直线![]() 代入③,整理得
代入③,整理得
![]()
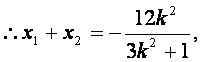
∵E(-2,0)是椭圆C的左焦点,
∴|MN|=|ME|+|NE|
=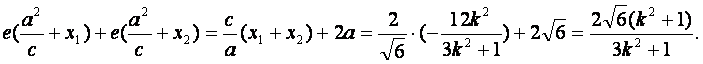
以下与解法一相同.
解法三:设M(![]() ),N(
),N(![]() ).
).
设直线![]() ,代入③,整理得
,代入③,整理得![]()
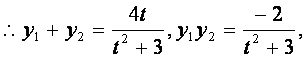
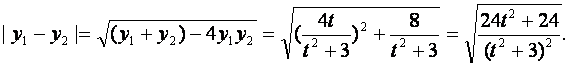
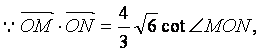
即 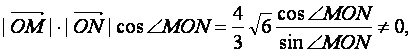
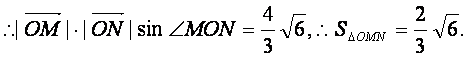
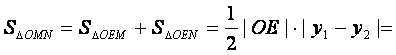
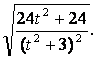
∴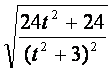 =
=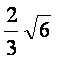 ,整理得
,整理得![]()
解得![]() 或
或![]()
故直线m的方程为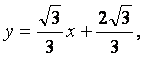 或
或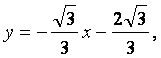 或
或![]()
经检验上述直线方程为![]()
所以所求直线方程为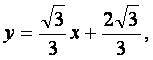 或
或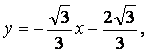 或
或![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。