解答题

17．（本小题满分12分）

  已知向量a=(，x+1)，b= (1-x，t)若函数=a·b在区间（-1，1）上

  是增函数，求t的取值范围

解:

解法一：依定义

则，

若在（-1，1）上是增函数，则在（-1，1）上可设≥0

∴≥0在（-1，1）上恒成立

考虑函数，由于的图象是对称轴为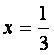，开口向上的抛物线，

故要使在（-1，1）上恒成立，即t≥5

而当t≥5时，在（-1，1）上满足>0，即在（-1，1）上是增函数

故t的取值范围是t≥5

解法二：依定义，

若在（-1，1）上是增函数，则在（-1，1）上可设≥0

∵的图象是开口向下的抛物线，

∴当且仅当，且时，

在（-1，1）上满足>0，即在（-1，1）上是增函数

故t的取值范围是t≥5