解答题
22.(本小题满分14分,第一小问满分4分,第二小问满分10分)
已知![]() ,函数
,函数![]()
![]()
⑴当![]() 时,求使
时,求使![]() 成立的
成立的![]() 的集合;
的集合;
⑵求函数![]() 在区间
在区间![]() 上的最小值
上的最小值![]()
(Ⅰ)由题意,![]()
当![]() 时,由
时,由![]() ,解得
,解得![]() 或
或![]() ;
;
当![]() 时,由
时,由![]() ,解得
,解得![]()
![]()
综上,所求解集为![]()
(Ⅱ)设此最小值为![]()
![]()
①当![]() 时,在区间[1,2]上,
时,在区间[1,2]上,![]() ,
,
因为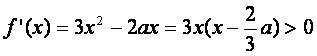 ,
,![]() ,
,
则![]() 是区间[1,2]上的增函数,所以
是区间[1,2]上的增函数,所以![]()
![]()
②当![]() 时,在区间[1,2]上,
时,在区间[1,2]上,![]() ,由
,由![]() 知
知
![]()
![]()
③当![]() 时,在区间[1,2]上,
时,在区间[1,2]上,![]()
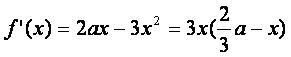
若![]() ,在区间(1,2)上,
,在区间(1,2)上,![]() ,则
,则![]() 是区间[1,2]上的增函数,
是区间[1,2]上的增函数,
所以![]()
![]()
若![]() ,则
,则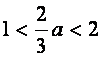
当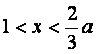 时,
时,![]() ,则
,则![]() 是区间[1,
是区间[1,![]() ]上的增函数,
]上的增函数,
当![]() 时,
时,![]() ,则
,则![]() 是区间[
是区间[![]() ,2]上的减函数,
,2]上的减函数,
因此当![]() 时,
时,![]() 或
或![]()
![]()
当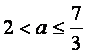 时,
时,![]() ,故
,故![]() ,
,
当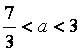 时,
时,![]() ,故
,故![]()
![]()
总上所述,所求函数的最小值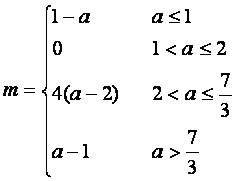
![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。