解答题
22.(本小题满分12分)
函数![]() 在区间(0,+∞)内可导,导函数
在区间(0,+∞)内可导,导函数![]() 是减函数,且
是减函数,且![]() 设
设
![]() 是曲线
是曲线![]() 在点(
在点(![]() )得的切线方程,并设
)得的切线方程,并设
函数![]()
(Ⅰ)用![]() 、
、![]() 、
、![]() 表示m;
表示m;
(Ⅱ)证明:当![]() ;
;
(Ⅲ)若关于![]() 的不等式
的不等式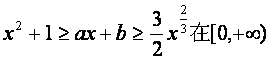 上恒成立,其中a、b为实数,
上恒成立,其中a、b为实数,
求b的取值范围及a与b所满足的关系.
本小题考查导数概念的几何意义,函数极值、最值的判定以及灵活运用数形结合
的思想判断函数之间的大小关系.考查学生的学习能力、抽象思维能力及综合运
用数学基本关系解决问题的能力.满分12分
(Ⅰ)解:![]() …………………………………………2分
…………………………………………2分
(Ⅱ)证明:令![]()
因为![]() 递减,所以
递减,所以![]() 递增,因此,当
递增,因此,当![]() ;
;
当![]() .所以
.所以![]() 是
是![]() 唯一的极值点,且是极小值点,可知
唯一的极值点,且是极小值点,可知![]() 的
的
最小值为0,因此![]() 即
即![]() …………………………6分
…………………………6分
(Ⅲ)解法一:![]() ,
,![]() 是不等式成立的必要条件,以下讨论设此条件成立.
是不等式成立的必要条件,以下讨论设此条件成立.
![]() 对任意
对任意![]() 成立的充要条件是
成立的充要条件是
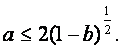
另一方面,由于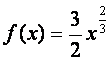 满足前述题设中关于函数
满足前述题设中关于函数![]() 的条件,
的条件,
利用(II)的结果可知,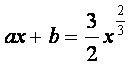 的充要条件是:过点(0,
的充要条件是:过点(0,![]() )与曲线
)与曲线
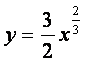 相切的直线的斜率大于
相切的直线的斜率大于![]() ,该切线的方程为
,该切线的方程为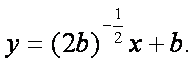
于是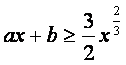 的充要条件是
的充要条件是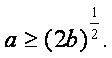 …………………………10分
…………………………10分
综上,不等式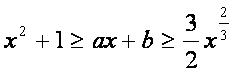 对任意
对任意![]() 成立的充要条件是
成立的充要条件是
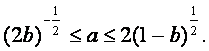 ①
①
显然,存在a、b使①式成立的充要条件是:不等式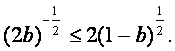 ②
②
有解、解不等式②得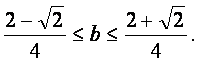 ③
③
因此,③式即为b的取值范围,①式即为实数在a与b所满足的关系.…………12分
(Ⅲ)解法二:![]() 是不等式成立的必要条件,以下讨论设此条件成立.
是不等式成立的必要条件,以下讨论设此条件成立.
![]() 对任意
对任意![]() 成立的充要条件是
成立的充要条件是
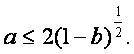 ………………………………………………………………8分
………………………………………………………………8分
令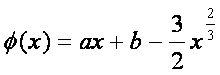 ,于是
,于是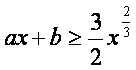 对任意
对任意![]() 成立的
成立的
充要条件是
![]() 由
由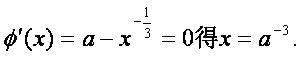
当![]() 时
时![]() 当
当![]() 时,
时,![]() ,所以,当
,所以,当![]() 时,
时,
![]() 取最小值.因此
取最小值.因此![]() 成立的充要条件是
成立的充要条件是![]() ,即
,即![]() ………10分
………10分
综上,不等式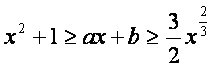 对任意
对任意![]() 成立的充要条件是
成立的充要条件是
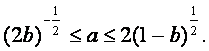 ①
①
显然,存在a、b使①式成立的充要条件是:不等式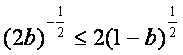 ②
②
有解、解不等式②得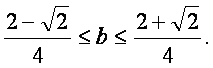
因此,③式即为b的取值范围,①式即为实数在a与b所满足的关系.…………12分
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。