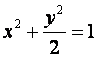 上,
上,解答题
(22)(本小题满分12分)
![]() 、
、![]() 、
、![]() 、
、![]() 四点都在椭圆
四点都在椭圆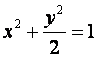 上,
上,![]() 为椭圆在
为椭圆在![]() 轴正半轴上的焦点.
轴正半轴上的焦点.
已知![]() 与
与![]() 共线,
共线,![]() 与
与![]() 共线,且
共线,且![]() .求四边形
.求四边形![]() 的面积
的面积
的最小值和最大值.
解:∵![]() .
即
.
即![]() .
.
当MN或PQ中有一条直线垂直于x轴时,另一条直线必垂直于y轴. 不妨设MN⊥y轴,则PQ⊥x轴![]()
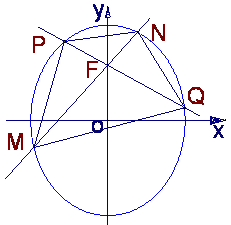 ∵F(0,
1) ∴MN的方程为:y=1,PQ的方程为:x=0
∵F(0,
1) ∴MN的方程为:y=1,PQ的方程为:x=0
分别代入椭圆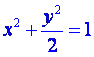 中得:|MN|=
中得:|MN|=![]() ,
|PQ|=2
,
|PQ|=2![]() .
.
S四边形PMQN=![]() |MN|·|PQ|=
|MN|·|PQ|=![]() ×
×![]() ×2
×2![]() =2
=2![]()
当MN,PQ都不与坐标轴垂直时,设MN的方程为y=kx+1 (k≠0),
代入椭圆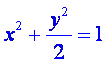 中得:(k2+2)x2+2kx-1=0,
中得:(k2+2)x2+2kx-1=0,
∴x1+x2=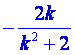 ,
x1·x2=
,
x1·x2=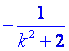
![]()
∴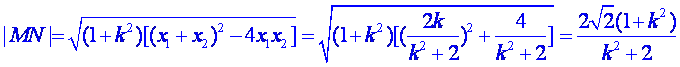
同理可得: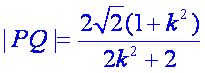
![]()
S四边形PMQN=![]() |MN|·|PQ|=
|MN|·|PQ|=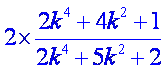 =
=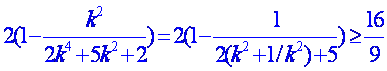
![]()
(当且仅当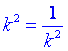 即
即![]() 时,取等号).
时,取等号).
又S四边形PMQN =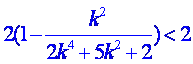 ,∴此时
,∴此时![]() S四边形PMQN
S四边形PMQN![]()
![]()
综上可知:(S四边形PMQN )max=2, (S四边形PMQN )min=![]()
![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。