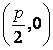解答题

 (22) （本小题满分14分）已知动圆过定点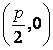，且与直线相切，其中.

（I）求动圆圆心的轨迹的方程；

（II）设A、B是轨迹上异于原点的两个不同点，直线和的倾斜角分别

为和，当变化且时，证明直线恒过定点，并求出该定点的坐标

（考查知识点:圆锥曲线）

解：（I）如图，设为动圆圆心，为记为，过点作直线的垂线，

垂足为，由题意知：即

动点到定点与定直线的距离相等，

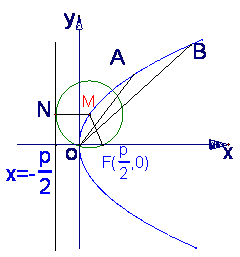
由抛物线的定义知，点的轨迹为抛物线，

其中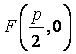为焦点，为准线，

所以轨迹方程为；

（II）如图，设，由题意得，

又直线OA,OB的倾斜角满足，故，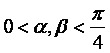

所以直线的斜率存在，

否则，OA,OB直线的倾斜角之和为

从而设AB方程为，显然，

将与联立消去，得

由韦达定理知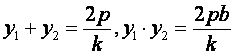①

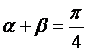由，得1＝==

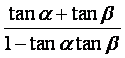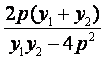
将①式代入上式整理化简可得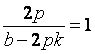：，所以，

此时，直线的方程可表示为即

所以直线恒过定点.