三、解答题

（21）（本大题满分12分）

     已知函数，其中是的导函数

（Ⅰ）对满足的一切的值，都有，求实数的取值范围；

（Ⅱ）设，当实数在什么范围内变化时，函数的图象与

直线只有一个公共点

本小题主要考察函数的单调性、导数的应用、解不等式等基础知识，

以及推理能力、运算能力和综合运用数学知识解决问题的能力。满分12分。

解：（Ⅰ）由题意

         令，

对，恒有，即

∴  即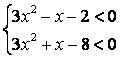

解得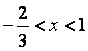

故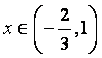时，对满足的一切的值，都有

（Ⅱ）

①当时，的图象与直线只有一个公共点

②当时，列表： 

∴。

又因为的值域是，且在上单调递增

∴当时函数的图象与直线只有一个公共点。

当时，恒有

由题意得

即

解得

综上，的取值范围是