三、解答题

22．（本小题满分14分）

已知函数

（Ⅰ）若，试确定函数的单调区间；

（Ⅱ）若，且对于任意，恒成立，试确定实数的取值范围；

（Ⅲ）设函数，求证：．

本小题主要考查函数的单调性、极值、导数、不等式等基本知识，考查运用导数

研究函数性质的方法，考查分类讨论、化归以及数形结合等数学思想方法，考查

分析问题、解决问题的能力．满分14分．

解：（Ⅰ）由得，所以．

       由得，故的单调递增区间是，

       由得，故的单调递减区间是．

       （Ⅱ）由可知是偶函数．

       于是对任意成立等价于对任意成立．

       由得．

       ①当时，．

       此时在上单调递增．

       故，符合题意．

       ②当时，．

       当变化时的变化情况如下表：

由此可得，在上，．

依题意，，又．

综合①，②得，实数的取值范围是．

（Ⅲ），

，

，

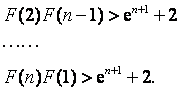
由此得，

故．