解答题
22. (本小题满分14分)
椭圆的中心是原点O,它的短轴长为![]() ,相应于焦点F(c,0)(
,相应于焦点F(c,0)(![]() )
)
的准线![]() 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点。
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点。
(1)求椭圆的方程及离心率;
(2)若![]() ,求直线PQ的方程;
,求直线PQ的方程;
(3)设![]() (
(![]() ),过点P且平行于准线
),过点P且平行于准线![]() 的直线与椭圆相交于
的直线与椭圆相交于
另一点M,证明![]() 。
。
本小题主要考查椭圆的标准方程和几何性质,直线方程,平面向量的计算,
曲线和方程的关系等解析几何的基本思想方法和综合解题能力。满分14分。
(1)解:由题意,可设椭圆的方程为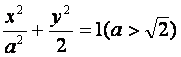 。
。
由已知得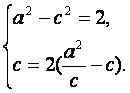
解得![]()
所以椭圆的方程为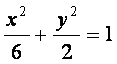 ,离心率
,离心率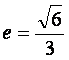 。
。
(2)解:由(1)可得A(3,0)。
设直线PQ的方程为![]() 。由方程组
。由方程组
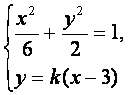
得![]()
依题意![]() ,得
,得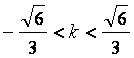 。
。
设![]() ,则
,则
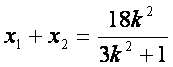 ,
①
,
①
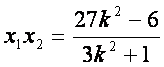 。
②
。
②
由直线PQ的方程得![]() 。于是
。于是
![]() 。
③
。
③
∵![]() ,∴
,∴![]() 。
④
。
④
由①②③④得![]() ,从而
,从而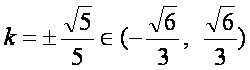 。
。
所以直线PQ的方程为![]() 或
或![]()
(2)证明:![]() 。由已知得方程组
。由已知得方程组

注意![]() ,解得
,解得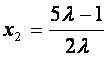
因![]() ,故
,故
![]()
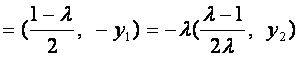 。
。
而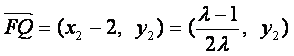 ,所以
,所以
![]() 。
。
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。