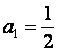解答题

全国卷Ⅰ(文)

（21）（本大题满分12分）

设正项等比数列的首项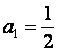，前n项和为，且

（Ⅰ）求的通项；

（Ⅱ）求的前n项和

解答

全国卷Ⅱ(文)

（21）（本小题满分14分）

设为实数，函数．

（Ⅰ）求的极值；

（Ⅱ）当在什么范围内取值时，曲线与轴仅有一个交点．

解答

全国卷Ⅲ(文)

(21) (本小题满分12分)

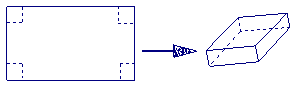用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去

一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为

多少时,容器的容积最大?最大容积是多少?

解答

北京卷(文)

（19）（本小题共14分）

    已知函数．

  (I)求的单调递减区间；

  (Ⅱ)若在区间[一2，2]上的最大值为20，求它在该区间上的最小值.

解答

天津卷(文)

(21)(本小题满分14分)

已知mÎR，设P：和是方程的两个实根，不等式

 对任意实数Î[-1,1]恒成立；

Q：函数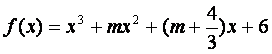在(－¥,+¥)上有极值

 求使P正确且Q正确的m的取值范围

解答

上海卷(文)

21.（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分6分，

第3小题满分6分

已知抛物线的焦点为F，A是抛物线上横坐标为4.且位于轴上

方的点，A到抛物线准线的距离等于5过A作AB垂直于轴，垂足为B，OB的中点为M

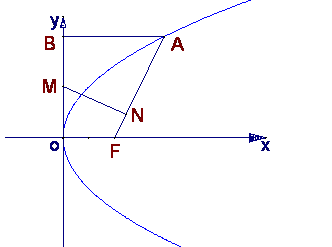（1）求抛物线方程；

（2）过M作，垂足为N，求点N的坐标；

（3）以M为圆心，MB为半径作圆M，当是轴

上一动点时，讨论直线AK与圆M的位置关系

解答

辽宁卷

21．（本小题满分14分）

已知椭圆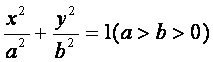的左、右焦点分别是F1（－c，0）、F2（c，0），

Q是椭圆外的动点，满足点P是线段F1Q与该椭圆的交点，点T在线段F2Q上，

并且满足

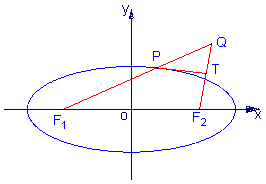   （Ⅰ）设为点P的横坐标，证明；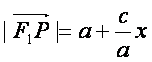

   （Ⅱ）求点T的轨迹C的方程；

   （Ⅲ）试问：在点T的轨迹C上，是否存在点M，

         使△F1MF2的面积S=若存在，求∠F1MF2

         的正切值；若不存在，请说明理由.

解答

江苏卷

23.（本小题满分14分，第一小问满分2分，第二.第三小问满分各6分）

设数列的前项和为，已知，且

    ，其中A.B为常数

  ⑴求A与B的值；

  ⑵证明：数列为等差数列；

  ⑶证明：不等式对任何正整数都成立

解答

浙江卷(文)

19．如图，已知椭圆的中心在坐标原点，焦点在x轴上，长轴A1A2的长为4，

左准线与x轴的交点为M，|MA1|∶|A1F1|＝2∶1．

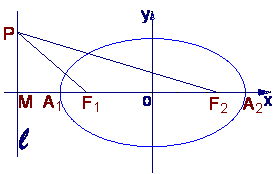   (Ⅰ)求椭圆的方程；

   (Ⅱ)若点P在直线上运动，求∠F1PF2的最大值．

    解答

福建卷(文)

21．（本小题满分12分）

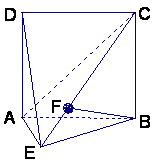  如图，直二面角D—AB—E中，四边形ABCD是边长为2的正方形，AE=EB，

  F为CE上的点，且BF⊥平面ACE.

  （Ⅰ）求证AE⊥平面BCE；

  （Ⅱ）求二面角B—AC—E的大小；

  （Ⅲ）求点D到平面ACE的距离.

     解答

湖北卷(文)

21．（本小题满分12分）

      某会议室用5盏灯照明，每盏灯各使用灯泡一只，且型号相同.假定每盏灯

    能否正常照明只与灯泡的寿命有关，该型号的灯泡寿命为1年以上的概率为p1，

    寿命为2年以上的概率为p2.从使用之日起每满1年进行一次灯泡更换工作，只更换

    已坏的灯泡，平时不换

   （Ⅰ）在第一次灯泡更换工作中，求不需要换灯泡的概率和更换2只灯泡的概率；

   （Ⅱ）在第二次灯泡更换工作中，对其中的某一盏灯来说，求该盏灯需要更换灯泡

    的概率；

   （Ⅲ）当p1=0.8，p2=0.3时，求在第二次灯泡更换工作，至少需要更换4只灯泡

    的概率（结果保留两个有效数字）

解答

湖南卷(文)

20．（本小题满分14分）

某单位组织4个部门的职工旅游，规定每个部门只能在韶山、衡山、张家界

3个景区中任选一个，假设各部门选择每个景区是等可能的.

   （Ⅰ）求3个景区都有部门选择的概率；

   （Ⅱ）求恰有2个景区有部门选择的概率

解答

广东卷

19．（本小题满分14分）

设函数，

且在闭区间[0，7]上，只有

   （Ⅰ）试判断函数的奇偶性；

   （Ⅱ）试求方程在闭区间[－2005，2005]上的根的个数，并证明你的结论.

解答

重庆卷(文)

21．（本小题满分12分）

已知中心在原点的双曲线C的右焦点为（2，0），右顶点为

   （1）求双曲线C的方程；

   （2）若直线与双曲线C恒有两个不同的交点A和B，且

（其中O为原点）. 求k的取值范围.

     解答

山东卷(文)

(21) （本小题满分12分）已知数列的首项前项和为，

且

（I）证明数列是等比数列；

（II）令，求函数在点处的导数

解答

江西卷(文)

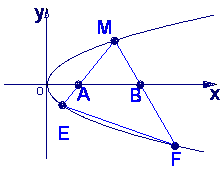
21．（本小题满分12分）

如图，M是抛物线上y2=x上的一点，动弦ME、MF分别交x轴于A、B两点，且MA=MB.

   （1）若M为定点，证明：直线EF的斜率为定值；

   （2）若M为动点，且∠EMF=90°，求△EMF的重心G的轨迹方程.

解答