 17.(本题满分12分)已知长方体
17.(本题满分12分)已知长方体解答题
 17.(本题满分12分)已知长方体
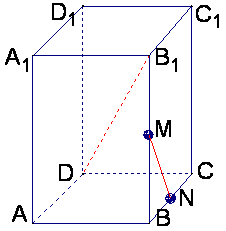
17.(本题满分12分)已知长方体![]() 中,M.N分别是
中,M.N分别是![]() 和BC的中点,
和BC的中点,
AB=4,AD=2,![]() 与平面ABCD所成角的大小为
与平面ABCD所成角的大小为![]() ,求异面直线
,求异面直线![]() 与MN所成角
与MN所成角
的大小![]() (结果用反三角函数值表示)
(结果用反三角函数值表示)
[解]联结B1C,由M.N分别是BB1和BC的中点,得B1C∥MN,
∴∠DB1C就是异面直线B1D与MN所成的角.
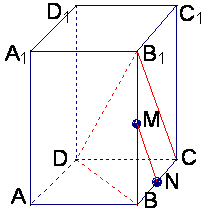 联结BD,在Rt△ABD中,可得BD=2
联结BD,在Rt△ABD中,可得BD=2![]() ,又BB1⊥平面ABCD,
∠B1DB是B1D与
,又BB1⊥平面ABCD,
∠B1DB是B1D与
平面ABCD所成的角, ∴∠B1DB=60°.
在Rt△B1BD中, B1B=BDtan60°=2![]() ,
,
又DC⊥平面BB1C1C, ∴DC⊥B1C,
在Rt△DB1C中, tan∠DB1C=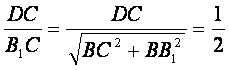 ,
,
∴∠DB1C=arctan![]() .
.
即异面直线B1D与MN所成角的大小为arctan![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。