解答题
(22)(本小题满分14分)
设函数![]() .
.
(Ⅰ)证明![]() ,其中为k为整数;
,其中为k为整数;
(Ⅱ)设![]() 为
为![]() 的一个极值点,证明
的一个极值点,证明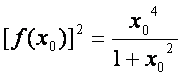 ;
;
(Ⅲ)设![]() 在(0,+∞)内的全部极值点按从小到大的顺序排列
在(0,+∞)内的全部极值点按从小到大的顺序排列![]() ,
,
证明
解:(Ⅰ)证明:由函数![]() 的定义,对任意整数
的定义,对任意整数![]() ,有
,有
![]()
![]() .
.
(Ⅱ)证明:函数![]() 在定义域
在定义域![]() 上可导,
上可导,![]() ①
①
令![]() ,得
,得![]() .
.
显然,对于满足上述方程的![]() 有
有![]() ,
,
上述方程化简为![]() .此方程一定有解.
.此方程一定有解.
![]() 的极值点
的极值点![]() 一定满足
一定满足![]() .
.
由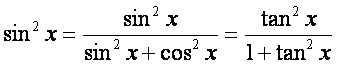 ,得
,得 .
.
因此, .
.
(Ⅲ)证明:设![]() 是
是![]() 的任意正实数根,即
的任意正实数根,即![]() ,
,
则存在一个非负整数![]() ,使
,使 ,即
,即![]() 在第二或第四象限内.
在第二或第四象限内.
由①式,![]() 在第二或第四象限中的符号可列表如下:
在第二或第四象限中的符号可列表如下:
|
|
|
|
|
|
|
|
|
- |
0 |
+ |
|
|
+ |
0 |
- |
|
所以满足![]() 的正根
的正根![]() 都为
都为![]() 的
的
极值点.
由题设条件,![]() ,
,![]() ,…,
,…,![]() ,…为方程
,…为方程![]() 的全部正实数根且满足
的全部正实数根且满足
![]() ,
,
那么对于![]() ,
,
![]() . ②
. ②
由于  ,
, ,
,
则 ,
,
由于![]() ,由②式知
,由②式知![]() .
.
由此可知![]() 必在第二象限,
必在第二象限,
即![]() . 综上,
. 综上,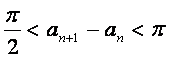 .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。