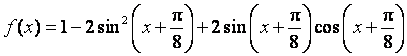．求：三、解答题
16．（本小题满分12分）
已知函数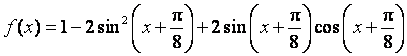．求：
（I）函数
的最小正周期；
（II）函数
的单调增区间．
17．（本小题满分12分）
某地区为下岗人员免费提供财会和计算机培训，以提高下岗人员的再就业能力，
每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训，已知参加
过财会培训的有60%，参加过计算机培训的有75%，假设每个人对培训项目的选
择是相互独立的，且各人的选择相互之间没有影响．
（I）任选1名下岗人员，求该人参加过培训的概率；
（II）任选3名下岗人员，求这3人中至少有2人参加过培养的概率．
18．（本小题满分12分）
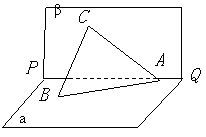
如图3，已知直二面角
，
，
，
，
，
，
直线
和平面
所成的角为
．
（I）证明
；
（II）求二面角
的大小．
19．（本小题满分13分）
已知双曲线
的右焦点为
，过点的动直线与双曲线相交于
两点，
点
的坐标是
．
（I）证明
，
为常数；
（II）若动点
满足
（其中
为坐标原点），求点的轨迹方程．
20．（本小题满分13分）
设
是数列
（
）的前
项和，
，且
，
，
．
（I）证明：数列
（
）是常数数列；
（II）试找出一个奇数
，使以18为首项，7为公比的等比数列
（
）中
的所有项都是数列中的项，并指出
是数列
中的第几项．
21．（本小题满分13分）
已知函数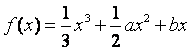
在区间
，
内各有一个极值点．
（I）求
的最大值；
（II）当
时，设函数
在点
处的切线为
，若
在点
处穿过
函数
的图象（即动点在点
附近沿曲线
运动，经过点时，从的一侧
进入另一侧），求函数
的表达式．