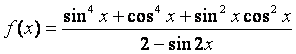 的最小正周期、最大值和最小值.
的最小正周期、最大值和最小值.2004年
解答题
17.(本小题满分12分)
求函数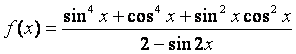 的最小正周期、最大值和最小值.
的最小正周期、最大值和最小值.
18.(本小题满分12分)
一接待中心有A、B、C、D四部热线电话,已知某一时刻电话A、B占线的
概率均为0.5,电话C、D占线的概率均为0.4,各部电话是否占线相互之间
没有影响.假设该时刻有ξ部电话占线.试求随机变量ξ的概率分布和它的期望.
19.(本小题满分12分)
已知![]() 求函数
求函数![]() 的单调区间.
的单调区间.
20.(本小题满分12分)
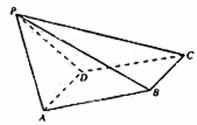
如图,已知四棱锥 P—ABCD,PB⊥AD侧面PAD为边长等于2的正三角形,
底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°.
(I)求点P到平面ABCD的距离,
(II)求面APB与面CPB所成二面角的大小.
21.(本小题满分12分)
设双曲线C: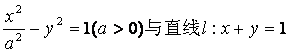 相交于两个不同的点A、B.
相交于两个不同的点A、B.
(I)求双曲线C的离心率e的取值范围:
(II)设直线l与y轴的交点为P,且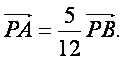 求a的值.
求a的值.
22.(本小题满分14分)
已知数列![]() ,且a2k=a2k-1+(-1)k,
a2k+1=a2k+3k,
,且a2k=a2k-1+(-1)k,
a2k+1=a2k+3k,
其中k=1,2,3,…….
(I)求a3, a5;
(II)求{ an}的通项公式.
2005年
解答题
(17)(本大题满分12分)
设函数![]() 图像的一条对称轴是直线
图像的一条对称轴是直线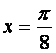
![]()
(Ⅰ)求![]() ;
;
(Ⅱ)求函数![]() 的单调增区间;
的单调增区间;
(Ⅲ)证明直线![]() 于函数
于函数![]() 的图像不相切
的图像不相切![]()
(18)(本大题满分12分)
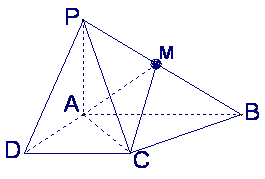 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,![]() 底面ABCD,
底面ABCD,
且PA=AD=DC=![]() AB=1,M是PB的中点
AB=1,M是PB的中点![]()
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小![]()
(19)(本大题满分12分)
设等比数列![]() 的公比为
的公比为![]() ,前n项和
,前n项和![]()
![]()
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)设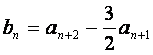 ,记
,记![]() 的前n项和为
的前n项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小
的大小![]()
(20)(本大题满分12分)
9粒种子分种在3个坑内,每坑3粒,每粒种子发芽的概率为![]() ,若一个坑内至少
,若一个坑内至少
有1粒种子发芽,则这个坑不需要补种; 若一个坑内的种子都没发芽,则这个坑
需要补种![]() 假定每个坑至多补种一次,每补种1个坑需10元,用ξ表示补种费用,
假定每个坑至多补种一次,每补种1个坑需10元,用ξ表示补种费用,
写出ξ的分布列并求ξ的数学期望![]() (精确到
(精确到![]() )
)
(21)(本大题满分14分)
已知椭圆的中心为坐标原点O,焦点在![]() 轴上,斜率为1且过椭圆右焦点F的直线
轴上,斜率为1且过椭圆右焦点F的直线
交椭圆于A、B两点,![]() 与
与![]() 共线
共线![]()
(Ⅰ)求椭圆的离心率;
(Ⅱ)设M为椭圆上任意一点,且![]() ,证明
,证明![]() 为定值
为定值![]()
(22)(本大题满分12分)
(Ⅰ)设函数![]() ,求
,求![]() 的最小值;
的最小值;
(Ⅱ)设正数![]() 满足
满足![]() ,证明
,证明
![]()
2006
解答题
(17)(本小题满分12分)
![]() 的三个内角为A、B、C,求当A为何值时
的三个内角为A、B、C,求当A为何值时![]() 取得最大值,
取得最大值,
并求出这个最大值。
(18)(本小题满分12分)
A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验.每个试验组由4只
小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效,若在一个试验组中,
服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组,设每只小
白鼠服用A有效的概率为![]() ,服用B有效的概率为
,服用B有效的概率为![]() 。
。
(Ⅰ)求一个试验组为甲类组的概率。
(Ⅱ)观察3个试验组,用![]() 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求![]() 的分布列和数
的分布列和数
学期望。
(19)(本小题满分12分)
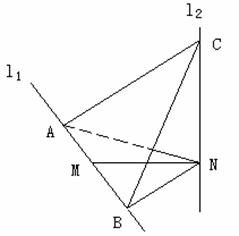
如图,l1、l2是互相垂直的异面直线,MN是它们的公垂线段,点A、B在l1上,C在
l2上,AM=MB=MN。
(Ⅰ)证明![]() ;
;
(Ⅱ)若![]() ,求NB与平面ABC所成角的余弦值。
,求NB与平面ABC所成角的余弦值。
(20)(本小题满分12分)
在平面直角坐标系xOy中,有一个以![]() 和
和![]() 为焦点、离心率为
为焦点、离心率为![]() 的
的
椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与x、y轴的
交点分别为A、B,且向量![]() ,求:
,求:
(Ⅰ)点M的轨迹方程;
(Ⅱ)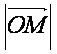 的最小值。
的最小值。
(21)(本小题满分14分)
已知函数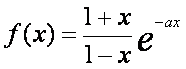 .
.
(Ⅰ)设![]() 讨论
讨论![]() 的单调性;
的单调性;
(Ⅱ)若对任意![]() 恒有
恒有![]() ,求a的取值范围。
,求a的取值范围。
(22)(本小题满分12分)
设数列{an}的前n项和
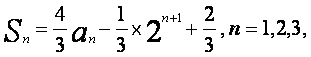 …。
…。
(Ⅰ)求首项a1与通项an;
(Ⅱ)设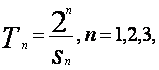 …,证明:
…,证明: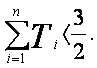
2007年
解答题
(17)(本小题满分10分)
设锐角三角形![]() 的内角
的内角![]() 的对边分别为
的对边分别为![]() ,
,![]() .
.
(Ⅰ)求![]() 的大小;
的大小;
(Ⅱ)求![]() 的取值范围.
的取值范围.
(18)(本小题满分12分)
某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为
的分布列为
|
|
1 |
2 |
3 |
4 |
5 |
|
|
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润
为250元;分4期或5期付款,其利润为300元.![]() 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(Ⅰ)求事件![]() :“购买该商品的3位顾客中,至少有1位采用1期付款”的概率
:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率![]() ;
;
(Ⅱ)求![]() 的分布列及期望
的分布列及期望![]() .
.
(19)(本小题满分12分)
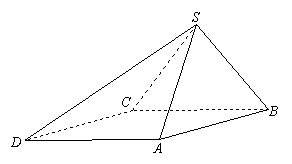 四棱锥
四棱锥![]() 中,底面
中,底面![]() 为平行四边形,侧面
为平行四边形,侧面![]() 底面
底面![]() .已知
.已知![]() ,
,
![]() ,
,![]() ,
,![]() .
.
(Ⅰ)证明![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
(20)(本小题满分12分)
设函数![]() .
.
(Ⅰ)证明:![]() 的导数
的导数![]() ;
;
(Ⅱ)若对所有![]() 都有
都有![]() ,求
,求![]() 的取值范围.
的取值范围.
(21)(本小题满分12分)
已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() .过
.过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,
两点,
过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且
两点,且![]() ,垂足为
,垂足为![]() .
.
(Ⅰ)设![]() 点的坐标为
点的坐标为![]() ,证明:
,证明: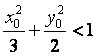 ;
;
(Ⅱ)求四边形![]() 的面积的最小值.
的面积的最小值.
(22)(本小题满分12分)
已知数列![]() 中
中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 中
中![]() ,
,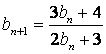 ,
,![]() ,
,
证明:![]() ,
,![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。