三、解答题
(18)(本题14分)已知![]() 的周长为
的周长为![]() ,且
,且![]() .
.
(I)求边![]() 的长;
的长;
(II)若![]() 的面积为
的面积为![]() ,求角
,求角![]() 的度数.
的度数.
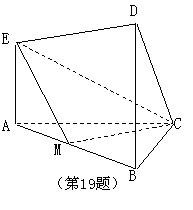
(19)(本题14分)在如图所示的几何体中,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() ,且
,且![]() ,
,![]() 是
是![]() 的中点.
的中点.
(I)求证:![]() ;
;
(II)求![]() 与平面
与平面![]() 所成的角.
所成的角.
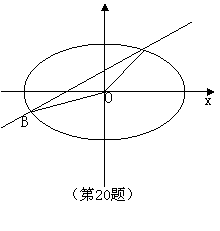
(20)(本题14分)如图,直线![]() 与椭圆
与椭圆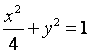
交于![]() 两点,
两点,
记![]() 的面积为
的面积为![]() .
.
(I)求在![]() ,
,![]() 的条件下,
的条件下,![]() 的最大值;
的最大值;
(II)当![]() ,
,![]() 时,求直线
时,求直线![]() 的方程.
的方程.
(21)(本题15分)已知数列![]() 中的相邻两项
中的相邻两项![]() 是关于
是关于![]() 的方程
的方程
![]() 的两个根,且
的两个根,且![]() .
.
(I)求![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(II)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)记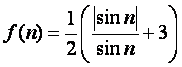 ,
,
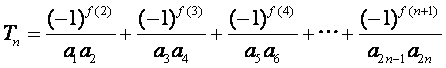 ,
,
求证:![]() .
.
(22)(本题15分)设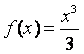 ,对任意实数
,对任意实数![]() ,记
,记 .
.
(I)求函数![]() 的单调区间;
的单调区间;
(II)求证:(ⅰ)当![]() 时,
时,![]()
![]() 对任意正实数
对任意正实数![]() 成立;
成立;
(ⅱ)有且仅有一个正实数![]() ,使得
,使得![]() 对任意正实数
对任意正实数![]() 成立.
成立.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。