解答题

全国卷Ⅰ(理)

（22）（本大题满分12分）

（Ⅰ）设函数，求的最小值；

（Ⅱ）设正数满足，证明

解答

全国卷Ⅱ(理)

（22）（本小题满分12分）

已知，函数．

（Ⅰ）当x为何值时，f(x)取得最小值？证明你的结论；

（Ⅱ）设f(x)在[-1,1]上是单调函数，求a的取值范围．

解答

全国卷Ⅲ(理)

22.（本小题满分12分）

 已知函数f(x)=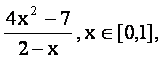

(1)求函数f(x)的单调区间和值域；

（2）设a≥1, 函数g(x)=x³-3a²x-2a, x∈[0,1], 若对于任意x₁∈[0,1],

总存在x₀∈[0,1], 使得g((x₀) =f(x₁)成立，求a的取值范围

解答

北京卷(理)

20 （本小题共14分）

设是定义在[0，1]上的函数，若存在，使得在[0，]上

单调递增，在[，1]单调递减，则称为[0，1]上的单峰函数，为峰点，

包含峰点的区间为含峰区间

对任意的[0，1]上的单峰函数，下面研究缩短其含峰区间长度的方法

（Ⅰ）证明：对任意的 , ,若，则（0，）为

含峰区间；若，则（，1）为含峰区间；

（Ⅱ）对给定的（0<<0.5），证明：存在,满足，

使得由（Ⅰ）确定的含峰区间的长度不大于0.5+;

(Ⅲ)选取, 由（Ⅰ）可确定含峰区间为（0，）或（，1），

在所得的含峰区间内选取,由与或与类似地可确定是一个新的含峰区间．

在第一次确定的含峰区间为（0，）的情况下，试确定的值，满足两两

之差的绝对值不小于0.02且使得新的含峰区间的长度缩短到0.34

（区间长度等于区间的右端点与左端点之差）

 解答

天津卷(理)

（22）（本小题满分14分）

设函数.

（Ⅰ）证明,其中为k为整数；

（Ⅱ）设为的一个极值点，证明；

（Ⅲ）设在(0,+∞)内的全部极值点按从小到大的顺序排列,

    证明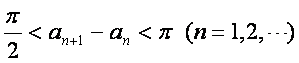

解答

上海卷(理)

22.在直角坐标平面中，已知点，，，，其中

n是正整数对平面上任一点，记为关于点的对称点，为关于点的

对称点，为关于点的对称点

（1）求向量的坐标；

（2）当点在曲线C上移动时，点的轨迹是函数的图像，其中是

以3位周期的周期函数，且当时，求以曲线C为图像的函数

在上的解析式；

（3）对任意偶数n，用n表示向量的坐标

解答

辽宁卷

22．（本小题满分12分）

 函数在区间（0，+∞）内可导，导函数是减函数，且 设

是曲线在点（）得的切线方程，并设

函数

   （Ⅰ）用、、表示m；

   （Ⅱ）证明：当；

   （Ⅲ）若关于的不等式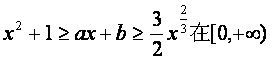上恒成立，其中a、b为实数，

         求b的取值范围及a与b所满足的关系.

     解答

浙江卷(理)

20．设点(，0)，和抛物线：y＝x2＋an x＋bn(n∈N*)，其中

a_n＝－2－4_n－，由以下方法得到：

   x₁＝1，点P₂(x₂，2)在抛物线C₁：y＝x₂＋a₁x＋b₁上，点A₁(x₁，0)到P₂的距离是

   A₁到C₁上点的最短距离，…，点在抛物线：y＝x₂＋a_n x＋b_n上，

   点(，0)到的距离是 到 上点的最短距离．

   (Ⅰ)求x₂及C₁的方程．

   (Ⅱ)证明{}是等差数列．

解答

福建卷(理)

22．（本小题满分14分）

已知数列{an}满足a1=a, an+1=1+我们知道当a取不同的值时，得到不同

的数列，如当a=1时，得到无穷数列：

（Ⅰ）求当a为何值时a4=0；

（Ⅱ）设数列{bn­}满足b1=－1, bn+1=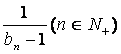，求证a取数列{bn}中的

任一个数，都可以得到一个有穷数列{an}；

（Ⅲ）若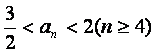，求a的取值范围.

解答

 湖北卷(理)

22．（本小题满分14分）

已知不等式，其中n为大于2的整数，表示

不超过的最大整数设数列{}的各项为正，且满足，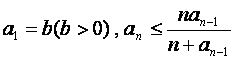

  （Ⅰ）证明：，；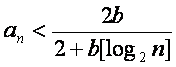

  （Ⅱ）猜测数列{}是否有极限？如果有，写出极限的值；

  （Ⅲ）试确定一个正整数N，使得当n>N时，对任意b>0，都有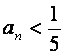

解答

湖南卷(理)

21．（本小题满分14分）

    已知函数f(x)＝lnx，g(x)＝ax2＋bx，a≠0

   （Ⅰ）若b＝2，且h(x)＝f(x)－g(x)存在单调递减区间，求a的取值范围；

   （Ⅱ）设函数f(x)的图象C1与函数g(x)图象C2交于点P、Q，过线段PQ的中

    点作x轴的垂线分别交C1，C2于点M、N，证明C1在点M处的切线与C2在点N

    处的切线不平行

解答

广东卷

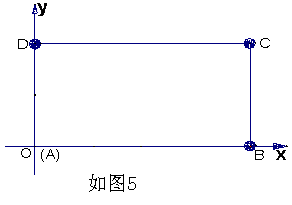
20．（本小题满分14分）

在平面直角坐标系中，已知矩形ABCD的长为2，宽为1，AB、AD边分别在x轴、

y轴的正半轴上，A点与坐标原点重合（如图5所示）.将矩形折叠，使A点落

在线段DC上.

    （Ⅰ）若折痕所在直线的斜率为k，

     试写出折痕所在直线的方程；

    （Ⅱ）求折痕的长的最大值.

     解答

重庆卷(理)

22．（本小题满分12分）

       数列{an}满足.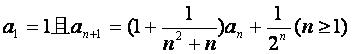

    （Ⅰ）用数学归纳法证明：；

  （Ⅱ）已知不等式，其中无理数

e=2.71828….

解答

山东卷(理)

(22) （本小题满分14分）已知动圆过定点，且与直线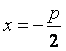相切，其中.

（I）求动圆圆心的轨迹的方程；

（II）设A、B是轨迹上异于原点的两个不同点，直线和的倾斜角分别

为和，当变化且为定值时，证明直线恒过定点，

并求出该定点的坐标

解答

江西卷(理)

22．（本小题满分14分）

  设抛物线的焦点为F，动点P在直线上运动，

  过P作抛物线C的两条切线PA、PB，且与抛物线C分别相切于A、B两点.

 （1）求△APB的重心G的轨迹方程.

 （2）证明∠PFA=∠PFB.

解答