 5.函数
5.函数福建(理)
选择题(每小题5分)
 5.函数
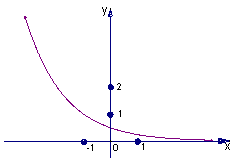
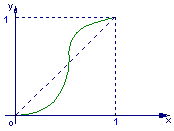
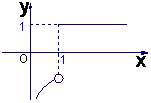
5.函数![]() 的图象如图,其中a、b为常数,则下列结论正确的是
的图象如图,其中a、b为常数,则下列结论正确的是
A.![]()
B.![]()
C.![]()
D.![]()
12.![]() 是定义在R上的以3为周期的奇函数,且
是定义在R上的以3为周期的奇函数,且![]() 在区间(0,6)
在区间(0,6)
内解的个数的最小值是
A.2 B.3 C.4 D.5
填空题(每小题4分)
16.把下面不完整的命题补充完整,并使之成为真命题:
若函数![]() 的图象与
的图象与![]() 的图象关于____对称,则函数
的图象关于____对称,则函数![]() =______
=______![]()
(注:填上你认为可以成为真命题的一件情形即可,不必考虑所有可能的情形).
解答题
19.(本小题满分12分)
已知函数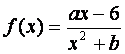 的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调区间.
浙江(理)
选择题(每小题5分)
3.设f(x)= ,则f[f(
,则f[f(![]() )]=(
)
)]=(
)
(A)
![]() (B)
(B)![]() (C)-
(C)-![]() (D)
(D)
![]()
填空题(每小题4分)
11.函数y= (x∈R,且x≠-2)的反函数是_________.
(x∈R,且x≠-2)的反函数是_________.
解答题
16.已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2=2x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)解不等式g(x)≥f(x)-|x-1|.
天津(理)
选择题(每小题4分)
(8)要得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象上所有的点的( )
的图象上所有的点的( )
(A)横坐标缩短到原来的![]() 倍(纵坐标不变),再向左平行移动
倍(纵坐标不变),再向左平行移动![]() 个单位长度
个单位长度
(B)横坐标缩短到原来的![]() 倍(纵坐标不变),再向右平行移动
倍(纵坐标不变),再向右平行移动![]() 个单位长度
个单位长度
(C)横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动![]() 个单位长度
个单位长度
(D)横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动![]() 个单位长度
个单位长度
(9)设![]() 是函数
是函数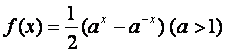 的反函数,则使
的反函数,则使![]() 成立的x的
成立的x的
取值范围为( )
(A)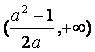 (B)
(B)
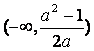 (C)
(C)
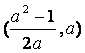 (D)
(D)
![]()
(10)若函数![]() 在区间
在区间 内单调递增,则a的取值
内单调递增,则a的取值
范围是( )
(A)![]() (B)
(B)
![]() (C)
(C) (D)
(D)![]()
填空题(每小题4分)
(16)设![]() 是定义在R上的奇函数,且
是定义在R上的奇函数,且![]() 的图象关于直线
的图象关于直线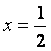 对称,则
对称,则
![]() =________________.
=________________.
解答题
(22)(本小题满分14分)
设函数![]() .
.
(Ⅰ)证明![]() ,其中为k为整数;
,其中为k为整数;
(Ⅱ)设![]() 为
为![]() 的一个极值点,证明
的一个极值点,证明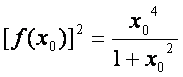 ;
;
(Ⅲ)设![]() 在(0,+∞)内的全部极值点按从小到大的顺序排列
在(0,+∞)内的全部极值点按从小到大的顺序排列![]() ,
,
证明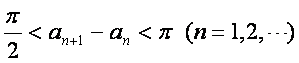
江苏
选择题(每小题5分)
2.函数![]() 的反函数的解析表达式为
的反函数的解析表达式为
A.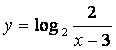 B.
B.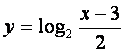 C.
C. D.
D.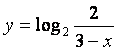
填空题(每小题4分)
15.函数![]() 的定义域为__________
的定义域为__________![]()
17.已知![]() 为常数,若
为常数,若![]() ,
,![]() ,
,
则![]() =__________
=__________![]()
解答题
22.(本小题满分14分,第一小问满分4分,第二小问满分10分)
已知![]() ,函数
,函数![]()
![]()
⑴当![]() 时,求使
时,求使![]() 成立的
成立的![]() 的集合;
的集合;
⑵求函数![]() 在区间
在区间![]() 上的最小值
上的最小值![]()
辽宁
选择题(每小题5分)
2.极限![]() 存在是函数
存在是函数![]() 在点
在点![]() 处连续的(
)
处连续的(
)
A.充分而不必要的条件 B.必要而不充分的条件
C.充要条件 D.既不充分也不必要的条件
5.函数![]() 的反函数是(
)
的反函数是(
)
A.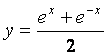 B.
B.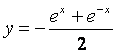 C.
C.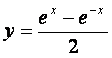 D.
D.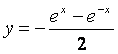
10.已知![]() 是定义在R上的单调函数,实数
是定义在R上的单调函数,实数![]() ,
,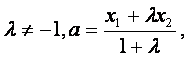
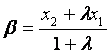 ,若
,若![]() ,则 (
)
,则 (
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.一给定函数![]() 的图象在下列图中,并且对任意
的图象在下列图中,并且对任意![]() ,由关系式
,由关系式
![]() 得到的数列
得到的数列![]() 满足
满足![]() ,则该函数的图象是(
)
,则该函数的图象是(
)
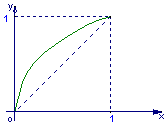
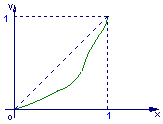
A B C D
解答题
 18.(本小题满分12分)
18.(本小题满分12分)
如图,在直径为1的圆O中,作一关于圆心对称、
邻边互相垂直的十字形,其中![]()
(Ⅰ)将十字形的面积表示为![]() 的函数;
的函数;
(Ⅱ)![]() 为何值时,十字形的面积最大?最大面积是多少?
为何值时,十字形的面积最大?最大面积是多少?
22.(本小题满分12分)
函数![]() 在区间(0,+∞)内可导,导函数
在区间(0,+∞)内可导,导函数![]() 是减函数,且
是减函数,且![]() 设
设
![]() 是曲线
是曲线![]() 在点(
在点(![]() )得的切线方程,并设
)得的切线方程,并设
函数![]()
(Ⅰ)用![]() 、
、![]() 、
、![]() 表示m;
表示m;
(Ⅱ)证明:当![]() ;
;
(Ⅲ)若关于![]() 的不等式
的不等式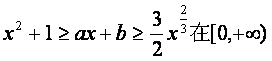 上恒成立,其中a、b为实数,
上恒成立,其中a、b为实数,
求b的取值范围及a与b所满足的关系.
重庆(理)
选择题(每小题5分)
3.若函数![]() 是定义在R上的偶函数,在
是定义在R上的偶函数,在![]() 上是减函数,且
上是减函数,且![]() ,
,
则使得![]() 的x的取值范围是(
)
的x的取值范围是(
)
A.![]() B.
B.![]() C.
C.![]() D.(-2,2)
D.(-2,2)
解答题
19.(本小题满分13分)
已知![]() ,讨论函数
,讨论函数![]() 的极值点的个数
的极值点的个数![]()
湖南(理)
选择题(每小题5分)
2.函数f(x)=![]() 的定义域是
的定义域是
A.![]() -∞,0]
B.[0,+∞
-∞,0]
B.[0,+∞![]() C.(-∞,0) D.(-∞,+∞)
C.(-∞,0) D.(-∞,+∞)
填空题(每小题4分)
14.设函数f(x)的图象关于点(1,2)对称,且存在反函数![]() ,
,
f (4)=0,则![]() =
.
=
.
15.设函数f (x)的图象与直线x =a,x =b及x轴所围成图形的面积称为
函数f(x)在[a,b]上的面积,已知函数y=sinnx在[0,![]() ]上的面积为
]上的面积为
![]() (n∈N*),(i)y=sin3x在[0,
(n∈N*),(i)y=sin3x在[0,![]() ]上的面积为 ;
]上的面积为 ;
(ii)y=sin(3x-π)+1在[![]() ,
,![]() ]上的面积为
.
]上的面积为
.
解答题
21.(本小题满分14分)
已知函数f(x)=lnx,g(x)=![]() ax2+bx,a≠0
ax2+bx,a≠0![]()
(Ⅰ)若b=2,且h(x)=f(x)-g(x)存在单调递减区间,求a的取值范围;
(Ⅱ)设函数f(x)的图象C1与函数g(x)图象C2交于点P、Q,过线段PQ的中
点作x轴的垂线分别交C1,C2于点M、N,证明C1在点M处的切线与C2在点N
处的切线不平行![]()
湖北(理)
选择题(每小题5分)
4.
函数![]() 的图象大致是
(
)
的图象大致是
(
)
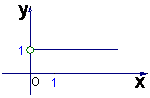
![]()
![]()
![]()
![]()
6.在![]() 这四个函数中,当
这四个函数中,当![]() 时,
时,
使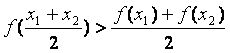 恒成立的函数的个数是
恒成立的函数的个数是
A.0 B.1 C.2 D.3
填空题(每小题4分)
16.某实验室需购某种化工原料106千克,现在市场上该原料有两种包装,
一种是每袋35千克,价格为140元;另一种是每袋24千克,价格为120元![]()
在满足需要的条件下,最少要花费 元![]()
解答题
17.(本小题满分12分)
已知向量a=(![]() ,x+1),b=
(1-x,t)
,x+1),b=
(1-x,t)![]() 若函数
若函数![]() =a·b在区间(-1,1)上
=a·b在区间(-1,1)上
是增函数,求t的取值范围![]()
广东
选择题(每小题5分)
6.函数![]() 是减函数的区间为
是减函数的区间为
A.![]() B.
B.![]() C.
C.![]() D.(0,2)
D.(0,2)
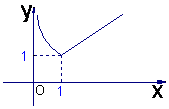
9.在同一平面直角坐标系中,函数![]() 和
和![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
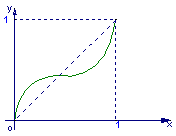
现将![]() 的图象沿
的图象沿![]() 轴向左平移2个单位,再沿
轴向左平移2个单位,再沿![]() 轴向上平移1个单位,所得的
轴向上平移1个单位,所得的
图象是由两条线段组成的折线(如图2所示),则函数![]() 的表达式为(
)
的表达式为(
)
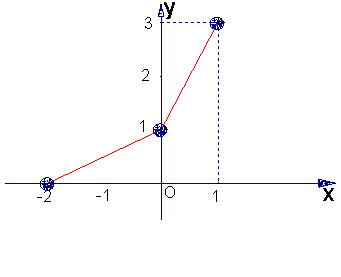 A.
A.
B.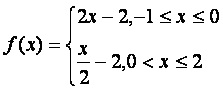
C.
D.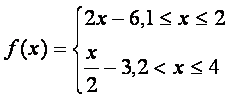
填空题(每小题4分)
11.函数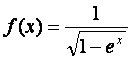 的定义域是
.
的定义域是
.
解答题
19.(本小题满分14分)
设函数![]() ,
,
且在闭区间[0,7]上,只有![]()
(Ⅰ)试判断函数![]() 的奇偶性;
的奇偶性;
(Ⅱ)试求方程![]() 在闭区间[-2005,2005]上的根的个数,并证明你的结论.
在闭区间[-2005,2005]上的根的个数,并证明你的结论.
北京(理)
选择题(每小题5分)
(8)函数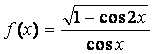
(A)在[0,![]() ),(
),(![]() ,
,![]() ]上递增,在[
]上递增,在[![]() ,
,![]() ),(
),(![]() ,2
,2![]() ]上递减
]上递减
(B)在[0,![]() ),[
),[![]() ,
,![]() )上递增,在(
)上递增,在(![]() ,
,![]() ],(
],(![]() ,2
,2![]() ]上递减
]上递减
(C)在(![]() ,
,![]() ],(
],(![]() ,2
,2![]() ]上递增,在[0,
]上递增,在[0,![]() ),[
),[![]() ,
,![]() )上递减
)上递减
(D)在[![]() ,
,![]() ),(
),(![]() ,2
,2![]() ]上递增,在[0,
]上递增,在[0,![]() ),(
),(![]() ,
,![]() ]上递减
]上递减
填空题(每小题5分)
(13) 对于函数![]() 定义域中任意的
定义域中任意的![]() (
(![]() ),有如下结论:
),有如下结论:
①![]() ;
②
;
②![]() ;
;
③ >0;
④
>0;
④ <
<
![]()
当![]() 时,上述结论中正确结论的序号是
时,上述结论中正确结论的序号是
![]()
解答题
15 (本小题共13分)
已知函数![]()
![]()
(I)求![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)若![]() 在区间[一2,2]上的最大值为20,求它在该区间上的最小值
在区间[一2,2]上的最大值为20,求它在该区间上的最小值![]()
20 (本小题共14分)
设![]() 是定义在[0,1]上的函数,若存在
是定义在[0,1]上的函数,若存在![]() ,使得
,使得![]() 在[0,
在[0,![]() ]上
]上
单调递增,在[![]() ,1]单调递减,则称
,1]单调递减,则称![]() 为[0,1]上的单峰函数,
为[0,1]上的单峰函数,![]() 为峰点,
为峰点,
包含峰点的区间为含峰区间![]()
对任意的[0,1]上的单峰函数![]() ,下面研究缩短其含峰区间长度的方法
,下面研究缩短其含峰区间长度的方法![]()
(Ⅰ)证明:对任意的![]()
![]() ,
, ![]() ,若
,若![]() ,则(0,
,则(0,![]() )为
)为
含峰区间;若![]() ,则(
,则(![]() ,1)为含峰区间;
,1)为含峰区间;
(Ⅱ)对给定的![]() (0<
(0<![]() <0.5),证明:存在
<0.5),证明:存在![]()
![]() ,满足
,满足![]() ,
,
使得由(Ⅰ)确定的含峰区间的长度不大于0.5+![]() ;
;
(Ⅲ)选取![]()
![]() ,
,![]() 由(Ⅰ)可确定含峰区间为(0,
由(Ⅰ)可确定含峰区间为(0,![]() )或(
)或(![]() ,1),
,1),
在所得的含峰区间内选取![]() ,由
,由![]() 与
与![]() 或
或![]() 与
与![]() 类似地可确定是一个新的含峰区间.
类似地可确定是一个新的含峰区间.
在第一次确定的含峰区间为(0,![]() )的情况下,试确定
)的情况下,试确定![]() 的值,满足两两
的值,满足两两
之差的绝对值不小于0.02且使得新的含峰区间的长度缩短到0.34![]()
(区间长度等于区间的右端点与左端点之差)![]()
上海(理)
选择题(每小题4分)
13.若函数![]() ,则该函数在
,则该函数在![]() 上是
上是
(A)单调递减无最小值 (B)单调递减有最小值
(C)单调递增无最大值 (D)单调递增有最大值
16.设定义域为为R的函数 ,则关于
,则关于![]() 的方程
的方程![]()
有7个不同的实数解得充要条件是
(A)![]() 且
且![]() (B)
(B)![]() 且
且![]()
(C)![]() 且
且![]() (D)
(D)![]() 且
且![]()
填空题(每小题4分)
1.函数![]() 的反函数
的反函数![]() ________________
________________![]()
10.函数![]() 的图像与直线
的图像与直线![]() 又且仅有两个不同
又且仅有两个不同
的交点,则![]() 的取值范围是____________
的取值范围是____________![]()
解答题
20.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分![]()
假设某市2004年新建住房400万平方米,其中有250万平方米是中低价房![]() 预计
预计
在今后的若干年内,该市每年新建住房面积平均比上一年增长8%,另外,每年新
建住房中,中低价房的面积均比上一年增加50万平方米![]() 那么,到那一年底,
那么,到那一年底,
(1)该市历年所建中低价房的累计面积(以2004年为累计的第一年)将首次不少
于4750万平方米?
(2)当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%?
21.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分,
第3小题满分6分![]()
对定义域是![]() .
.![]() 的函数
的函数![]() .
.![]() ,
,
规定:函数
![]()
(1)若函数 ,
,![]() ,写出函数
,写出函数![]() 的解析式;
的解析式;
(2)求问题(1)中函数![]() 的值域;
的值域;
(3)若![]() ,其中
,其中![]() 是常数,且
是常数,且![]() ,请设计一个定义域为R的函数
,请设计一个定义域为R的函数
![]() ,及一个
,及一个![]() 的值,使得
的值,使得![]() ,并予以证明
,并予以证明![]()
山东(理)
选择题(每小题5分)
(2)函数 的反函数的图象大致是
的反函数的图象大致是




(A) (B) (C) (D)
(3)已知函数 则下列判断正确的是
则下列判断正确的是
(A)此函数的最小正周期为![]() ,其图象的一个对称中心是
,其图象的一个对称中心是
(B) 此函数的最小正周期为![]() ,其图象的一个对称中心是
,其图象的一个对称中心是
(C) 此函数的最小正周期为![]() ,其图象的一个对称中心是
,其图象的一个对称中心是
(D) 此函数的最小正周期为![]() ,其图象的一个对称中心是
,其图象的一个对称中心是
(4)下列函数中既是奇函数,又是区间![]() 上单调递减的是
上单调递减的是
(A)![]() (B)
(B) ![]()
(C)  (D)
(D) 
(6)函数 若
若![]() 则
则![]() 的所有可能值为
的所有可能值为
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() ,
,![]() (D)
(D) ![]() ,
,![]()
解答题
(19) (本小题满分12分)
已知![]() 是函数
是函数![]() 的一个极值点,其中
的一个极值点,其中![]()
![]() .
.
(Ⅰ)求m与n的关系表达式;
(Ⅱ)求![]() 的单调区间;
的单调区间;
(Ⅲ)当![]() 时,函数
时,函数![]() 的图象上任意一点的切线斜率恒大于3m,
的图象上任意一点的切线斜率恒大于3m,
求m的取值范围![]()
江西(理)
选择题(每小题5分)
5.设函数![]() 为
为
A.周期函数,最小正周期为![]() B.周期函数,最小正周期为
B.周期函数,最小正周期为![]()
C.周期函数,数小正周期为![]() D.非周期函数
D.非周期函数
7.已知函数![]()
![]() ,
,
下面四个图象中![]() 的图象大致是
的图象大致是




A B C D
填空题(每小题4分)
13.若函数![]() 是奇函数,则a= .
是奇函数,则a= .
解答题
17.(本小题满分12分)
已知函数 (a,b为常数)且方程f(x)-x+12=0有两个实根
(a,b为常数)且方程f(x)-x+12=0有两个实根
为x1=3, x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;
全国卷(Ⅰ)理
选择题(每小题5分)
(8)设![]() ,二次函数
,二次函数![]() 的图像为下列之一
的图像为下列之一




则![]() 的值为
的值为
(A)![]() (B)
(B)![]() (C)
(C) (D)
(D)
(9)设![]() ,函数
,函数![]() ,则使
,则使![]() 的
的![]() 的取值范围是
的取值范围是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解答题
(22)(本大题满分12分)
(Ⅰ)设函数![]() ,求
,求![]() 的最小值;
的最小值;
(Ⅱ)设正数![]() 满足
满足![]() ,证明
,证明
![]()
全国卷(Ⅱ)理
选择题(每小题5分)
(3)函数![]() 的反函数是
的反函数是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
解答题
(17)(本小题满分12分)
设函数![]() ,求使
,求使![]() 的
的![]() 取值范围.
取值范围.
(22)(本小题满分12分)
已知![]() ,函数
,函数![]() .
.
(Ⅰ)当x为何值时,f(x)取得最小值?证明你的结论;
(Ⅱ)设f(x)在[-1,1]上是单调函数,求a的取值范围.
全国卷(Ⅲ)理
解答题
22.(本小题满分12分)
已知函数f(x)=
(1)求函数f(x)的单调区间和值域;
(2)设a≥1, 函数g(x)=x3-3a2x-2a, x∈[0,1], 若对于任意x1∈[0,1],
总存在x0∈[0,1],
使得g((x0)
=f(x1)成立,求a的取值范围![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。